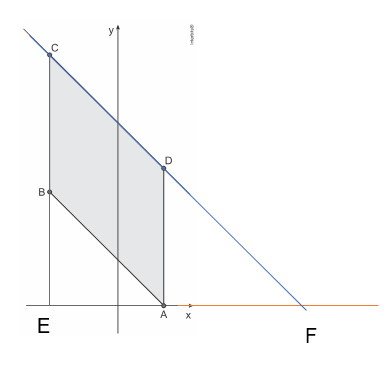
Considere o paralelogramo ABCD, com A(2,0), B= (-3,5) e o lado AD de medida igual a 6, conforme mostra a figura.
Devemos prolongar os lados do paralelogramo até intersectarem o eixo Ox (vide figura), como as coordenadas do ponto A e B são, respectivamente (2,0) e (-3,5), então o segmento AE mede 5 unidade e o segmento BE, também, mede 5 unidades, logo o triângulo AEB é retângulo e isósceles, como o lado CD é paralelo ao AB, então o triângulo ADF também é isósceles, no enunciado cita que o lado AD mede 2, logo o lado AF também mede 6, como o ponto A tem abscissa 2, mais seis unidades do lado AF, o ponto F tem abscissa 8.